안녕하세요! 여러분의 엑셀 업무 효율을 책임지는 블로거입니다. 😊 데이터 분석을 하다 보면 '상위 25% 실적은 얼마지?', '하위 그룹을 제외한 중간 값 범위는 어떻게 될까?' 와 같은 궁금증이 생길 때가 많죠? 이럴 때 사용하는 강력한 무기가 바로 사분위수(Quartile) 함수랍니다. 오늘은 비슷해 보이지만 결정적인 차이가 있는 QUARTILE.INC와 QUARTILE.EXC 함수에 대해 확실하게 알려드릴게요!
📌 [핵심] QUARTILE.INC는 전체 데이터(0%~100%)를 기준으로, QUARTILE.EXC는 양 끝 값을 제외한 데이터(0%와 100% 제외)를 기준으로 사분위수를 계산해요.
🤔 사분위수(Quartile), 그게 뭔가요?
엑셀 함수를 배우기 전에 '사분위수'가 뭔지 알아야겠죠? 어렵게 생각할 필요 없어요! 전체 데이터를 크기순으로 쫙~ 줄을 세운 뒤, 정확히 4등분 하는 위치의 값이라고 생각하면 돼요.
- 1사분위수 (Q1): 데이터의 하위 25%에 해당하는 값
- 2사분위수 (Q2): 데이터의 중간값(50%), 즉 MEDIAN 함수와 동일해요.
- 3사분위수 (Q3): 데이터의 상위 25% (전체 중 75%)에 해당하는 값
- 최솟값 (0%) / 최댓값 (100%)
이 값들을 이용하면 데이터가 어디에 집중적으로 분포되어 있는지 한눈에 파악할 수 있답니다.
🔎 QUARTILE.INC vs QUARTILE.EXC 함수 파헤치기
엑셀 2010 버전부터 사분위수 함수가 두 가지로 나뉘었어요. 이름 끝에 붙은 INC와 EXC가 바로 핵심 차이점이에요!
1. QUARTILE.INC 함수 (Inclusive: 포함)
가장 일반적이고 전통적인 사분위수 계산 방식이에요. INC는 Inclusive(포함하다)의 약자로, 최솟값(0%)과 최댓값(100%)을 포함해서 4등분 지점을 계산합니다.
함수 구문:
=QUARTILE.INC(array, quart)인수 설명:
- array: 사분위수를 구하려는 데이터 범위(필수)에요.
- quart: 어떤 사분위수 값을 반환할지 지정하는 숫자(필수)에요.
- 0: 최솟값 (0%)
- 1: 1사분위수 (25%)
- 2: 2사분위수 (50%, 중앙값)
- 3: 3사분위수 (75%)
- 4: 최댓값 (100%)
📝 노트: Excel 2007 및 이전 버전의 QUARTILE 함수와 완전히 동일한 기능의 함수에요. 하위 버전과의 호환성이 필요할 때 유용하죠.
2. QUARTILE.EXC 함수 (Exclusive: 제외)
이름에서 알 수 있듯이 EXC는 Exclusive(제외하다)의 약자에요. 즉, 최솟값(0%)과 최댓값(100%)을 계산 범위에서 제외하고 그 사이의 값들로만 사분위수를 구합니다.
함수 구문:
=QUARTILE.EXC(array, quart)인수 설명:
- array: 사분위수를 구하려는 데이터 범위(필수)에요.
- quart: 어떤 사분위수 값을 반환할지 지정하는 숫자(필수)에요.
- 1: 1사분위수 (25%)
- 2: 2사분위수 (50%, 중앙값)
- 3: 3사분위수 (75%)
📝 노트: quart 인수로 0이나 4를 입력하면 #NUM! 오류가 발생해요! 양 끝 값을 제외하기 때문이죠. 통계학적으로 더 엄밀한 분석이 필요할 때 사용됩니다.
🚀 실무 예제로 완벽 마스터하기
백문이 불여일견! 아래 영업팀의 월별 판매량 데이터를 가지고 두 함수의 차이와 활용법을 알아볼게요.
[예제 데이터]
제품명,월별 판매량
A제품,150
B제품,220
C제품,85
D제품,310
E제품,175
F제품,450
G제품,260
H제품,110
I제품,290
J제품,380
예제 1: 기본 사분위수 계산하기
먼저 각 함수의 1사분위수(하위 25%) 값을 구해볼까요? 판매량 데이터가 B2:B11에 있다고 가정할게요.
수식 : QUARTILE.INC 사용 (0, 100% 포함)
=QUARTILE.INC(B2:B11, 1)결과: 156.25

수식 : QUARTILE.EXC 사용 (0, 100% 제외)
=QUARTILE.EXC(B2:B11, 1)결과: 140
결과값이 다른 게 보이시나요? INC는 전체 10개 데이터를 기준으로 25% 지점을, EXC는 양 끝(최소와 최대) 값을 제외한 개념으로 25% 지점을 계산하기 때문에 이런 차이가 발생해요.
예제 2: 중급 - 핵심 데이터 구간(IQR) 분석하기
데이터 분석에서 중간 50%의 데이터가 어떻게 분포하는지 파악하는 것은 매우 중요해요. 이를 사분위수 범위(IQR, Interquartile Range)라고 하며, '3분위수 - 1분위수' 로 간단히 구할 수 있어요.
"우리 팀 판매량의 핵심적인 중간 50% 구간의 범위는 어떻게 될까?"
=QUARTILE.INC(B2:B11, 3) - QUARTILE.INC(B2:B11, 1)
결과: 148.75 (305 - 156.25)
해석: 우리 팀 판매량의 중간 50% 는 약 149 정도의 범위 안에서 움직이는군요!
예제 3: 고급 - 이상치(Outlier) 데이터 찾아내기
데이터를 분석할 때 평균을 왜곡하는 너무 크거나 작은 값, 즉 이상치를 찾아내는 건 필수에요. 사분위수는 이상치를 찾는 좋은 기준이 될 수 있습니다. (통계학적 기준 이상치: 1.5 x IQR)
"평균 실적을 왜곡하는 '특이 판매 실적'이 있었을까?"
ㄱ. IQR 값 계산: F2 셀에
=QUARTILE.INC(B2:B11, 3) - QUARTILE.INC(B2:B11, 1) //결과: 148.75
ㄴ. 하한/상한선 계산:
하한선:
=QUARTILE.INC(B2:B11, 1) - (1.5 * F2) //결과: -66.875상한선:
=QUARTILE.INC(B2:B11, 3) + (1.5 * F2) //결과: 528.125
ㄷ. 이상치 판별 (IF + OR 함수 조합):
=IF(OR(B2 < [하한선 값], B2 > [상한선 값]), "이상치", "정상")B2셀의 판매량 기준 이상치 판별 수식 :
=IF(OR(B2 < $F$5, B2 > $F$7), "이상치", "정상")
해석: 위 데이터에서는 상한선(528.125)과 하한선(-66.875)을 벗어나는 값이 없으므로 모든 판매량이 '정상' 범위에 속한다고 판단할 수 있어요. 만일, 판매량이 상한과 하한을 벗어나는 700 이나 -70 의 판매 제품이 있었다면 '이상치' 로 분류되었겠죠?
예제 4: 실무 활용 - 판매 실적 등급 나누기
사분위수를 기준으로 실적을 '우수', '보통', '부진'으로 자동 분류하여 성과 관리에 활용할 수 있어요.
"판매량 기준으로 직원들의 성과를 자동으로 나누고 싶어!"
수식: I2 셀에 아래 수식을 입력하고 아래로 쭉~ 드래그 해보세요. ($B$2:$B$11 처럼 절대 참조를 사용하는 것이 포인트!)
=IF(B2 >= QUARTILE.INC($B$2:$B$11, 3), "우수", IF(B2 >= QUARTILE.INC($B$2:$B$11, 1), "보통", "부진"))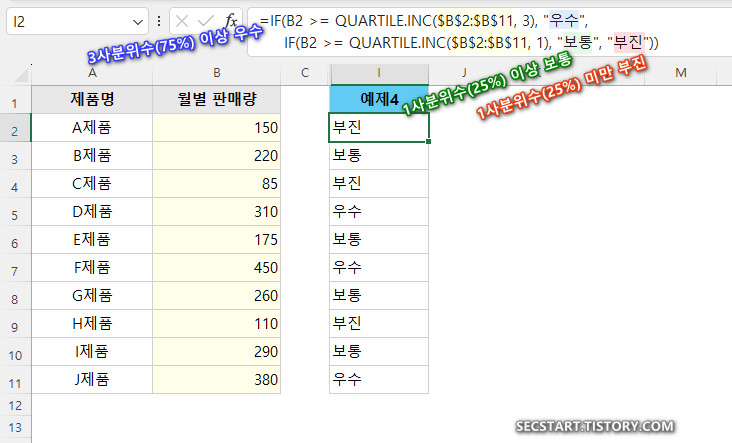
해석: 3사분위수(상위 25%) 이상이면 '우수', 1사분위수(하위 25%) 미만이면 '부진', 그 사이는 '보통'으로 자동 분류됩니다. 정말 편리하죠? 👍
💡 자주 발생하는 오류와 해결법
- #NUM! 오류:
- 원인 1: QUARTILE.EXC 함수에서 quart 인수로 0 또는 4를 입력했을 경우
- 원인 2: array로 지정한 데이터 범위가 비어있을 경우
- 해결: QUARTILE.EXC에서는 1, 2, 3만 사용하고, 데이터 범위에 값이 있는지 확인하세요.
- #VALUE! 오류:
- 원인: quart 인수에 숫자가 아닌 텍스트 등을 입력했을 경우
- 해결: quart 인수에는 0, 1, 2, 3, 4 (INC 기준) 중 숫자만 입력하세요.
🤝 함께 알아두면 좋은 친구 함수들
- PERCENTILE.INC / PERCENTILE.EXC: 사분위수(4등분)보다 더 세밀하게 백분위수(100등분)를 구하고 싶을 때 사용해요. QUARTILE의 확장판이죠!
- MEDIAN: 데이터의 정확한 중앙값을 구하며, QUARTILE.INC(범위, 2) 및 QUARTILE.EXC(범위, 2)와 동일한 결과를 반환해요.
- MIN / MAX: 각각 데이터의 최솟값과 최댓값을 구하며, QUARTILE.INC(범위, 0)과 QUARTILE.INC(범위, 4)와 동일해요.
💖 마무리하며
오늘은 엑셀 데이터 분석의 기초 체력이라고 할 수 있는 QUARTILE.INC와 QUARTILE.EXC 함수에 대해 배워봤습니다. 두 함수의 핵심 차이는 양 끝 값(0%, 100%)을 계산에 포함하느냐(INC), 제외하느냐(EXC) 라는 점, 이제 확실히 아시겠죠?
단순히 값만 구하는 것에서 나아가 오늘 배운 실무 예제처럼 데이터를 분류하고, 이상치를 찾아내고, 핵심 구간을 분석하는 데 활용한다면 여러분의 보고서 퀄리티는 한 단계 더 업그레이드될 거예요.
오늘 내용이 유용하셨다면 공감과 댓글 꼭 부탁드려요! 여러분의 작은 응원이 제게는 정말 큰 힘이 된답니다. 궁금한 점은 언제든 댓글로 질문해 주세요! 🤗
작성자: 마늘빵
📱 모바일에서 빠르게 보는 핵심 요약
✅ QUARTILE.INC vs QUARTILE.EXC 핵심 차이
- INC (포함): 0%, 25%, 50%, 75%, 100% 지점 계산 (전통 방식 : QUARTILE 과 동일)
- EXC (제외): 25%, 50%, 75% 지점만 계산 (양 끝 값 제외)
✅ 언제 뭘 쓸까?
- 일반적인 분석, 하위 버전 호환: QUARTILE.INC
- 통계적으로 더 엄밀한 분석: QUARTILE.EXC
✅ 실무 활용 KEY 3가지
- 핵심 구간(IQR) 찾기: =Q3 - Q1 (중간 50% 데이터 범위)
- 이상치(특이값) 찾기: 1.5 x IQR 규칙 활용
- 성과 등급 나누기: IF 함수와 조합해 사분위수로 '우수/보통/부진' 분류