✨ 엑셀 PEARSON 함수 완전 정복: 데이터 분석, 이젠 어렵지 않아요! (2025년 최신)

엑셀, 업무에서 정말 많이 사용하시죠? 📊 수많은 데이터 속에서 의미 있는 관계를 찾아내는 것은 마치 숨은그림찾기와 같을 때가 많은데요. 특히 두 데이터 집합 간의 관련성을 파악하는 것은 데이터 분석의 첫걸음이라고 할 수 있습니다.

 

📌 핵심은 바로 이것! 엑셀 PEARSON 함수를 사용하면 두 데이터 배열 간의 피어슨 곱 적률 상관 계수를 쉽고 빠르게 계산하여 데이터 간의 선형 관계를 파악할 수 있습니다!

 

"상관 계수? 그게 뭐지? 너무 어려운 거 아니야? 🤔" 라고 생각하실 수도 있지만, 전혀 걱정하지 마세요! 오늘 이 글을 통해 PEARSON 함수가 무엇인지, 어떻게 사용하는지, 그리고 실무에서 어떻게 활용할 수 있는지까지! 아주 쉽고 재미있게 알려드릴게요. 😊

 

💡 PEARSON 함수, 너는 누구냐?

PEARSON 함수는 두 개의 숫자 데이터 집합(배열)이 주어졌을 때, 이 두 집합 간의 선형적인 관계의 정도와 방향을 나타내는 피어슨 상관 계수(Pearson Correlation Coefficient)를 반환하는 함수예요. 이 값은 -1부터 1 사이의 값을 가지며, 다음과 같은 의미를 지닙니다.

• 1에 가까울수록: 두 데이터 집합 간에 강한 양의 선형 관계가 있음을 의미해요. 즉, 하나의 값이 증가하면 다른 값도 증가하는 경향이 뚜렷하다는 거죠. (예: 아이스크림 판매량과 기온 🍦☀️)
• -1에 가까울수록: 두 데이터 집합 간에 강한 음의 선형 관계가 있음을 의미해요. 하나의 값이 증가하면 다른 값은 감소하는 경향이 뚜렷하다는 뜻입니다. (예: 난방비와 외부 온도 🔥❄️)
• 0에 가까울수록: 두 데이터 집합 간에 선형적인 관계가 거의 없음을 의미해요. 두 데이터는 서로 큰 관련 없이 움직인다고 볼 수 있습니다.

쉽게 말해, "A 데이터가 변할 때 B 데이터는 얼마나 비슷하게 변하는가?"를 숫자로 보여주는 것이죠!

 

🛠️ PEARSON 함수 사용법: 이렇게 간단하다고?

PEARSON 함수의 구문은 아주 간단합니다.

구문:

PEARSON(array1, array2)

• array1: 첫 번째 숫자 데이터 집합 또는 배열입니다. (필수 요소)
• array2: 두 번째 숫자 데이터 집합 또는 배열입니다. (필수 요소)

📝 여기서 잠깐! 노트:

• array1과 array2는 숫자를 포함해야 하며, 텍스트, 논리값 또는 빈 셀은 계산에서 제외됩니다 (단, 0 값은 포함).
• 두 배열의 데이터 요소 개수가 동일해야 합니다. 만약 개수가 다르면 #N/A 오류가 발생해요!
• 어느 한 배열이라도 비어 있거나, 값의 표준 편차가 0이면 (즉, 모든 값이 동일하면) #DIV/0! 오류가 발생할 수 있습니다.

 

💼 실무 활용 예제: PEARSON 함수, 이렇게 써보세요!

자, 이제 실제 업무에서 PEARSON 함수를 어떻게 활용할 수 있는지 구체적인 예시를 통해 알아볼까요? 세 가지 시나리오를 준비했어요. 각 예제에 필요한 데이터는 CSV 텍스트 형식으로 제공해 드릴 테니, 직접 엑셀에 복사해서 사용해 보세요!

예제 1: 광고비와 매출액의 상관관계 분석

마케팅팀에서 광고 예산에 따른 매출액 변화를 분석하여 광고 효과를 측정하고 싶어 합니다.

데이터 (ad_sales.csv):

월,광고비(백만원),매출액(천만원)
1월,10,150
2월,12,180
3월,15,220
4월,11,160
5월,18,250
6월,20,280
7월,17,240
8월,13,190
9월,16,230
10월,19,270
11월,22,300
12월,25,350

엑셀 사용:

• A열에 '월', B열에 '광고비(백만원)', C열에 '매출액(천만원)' 데이터를 입력합니다.
• 상관 계수를 계산할 셀에 다음 수식을 입력합니다: =PEARSON(B2:B13, C2:C13)

예제1: 엑셀 PEARSON 함수 피어슨 상관계수 구하기

결과 해석:

만약 결과값이 0.95와 같이 1에 가깝게 나왔다면, 광고비와 매출액 사이에 매우 강한 양의 상관관계가 있다고 해석할 수 있습니다. 즉, 광고비를 늘리면 매출액도 증가하는 경향이 뚜렷하다는 의미가 됩니다.

 

예제 2: 근무 시간과 생산량의 관계 분석

생산팀에서 직원들의 월간 근무 시간과 해당 월의 제품 생산량 간의 관계를 파악하여 생산 효율성을 분석하고자 합니다.

데이터 (work_production.csv):

직원ID,월간근무시간,월간생산량(개)
EMP001,160,850
EMP002,165,880
EMP003,150,800
EMP004,170,920
EMP005,155,820
EMP006,180,950
EMP007,140,750
EMP008,175,930
EMP009,162,860
EMP010,158,840
EMP011,172,910
EMP012,145,780

엑셀 사용:

• A열에 '직원ID', B열에 '월간근무시간', C열에 '월간생산량(개)' 데이터를 입력합니다.
• 상관 계수를 계산할 셀에 다음 수식을 입력합니다: =PEARSON(B2:B13, C2:C13)


예제2: 엑셀 PEARSON 함수 근무시간 생산량 상관계수

결과 해석:

결과값이 예를 들어 0.88이라면 근무 시간과 생산량 간에 강한 양의 상관관계가 있다고 볼 수 있습니다. 근무 시간이 늘어날수록 생산량도 증가하는 경향이 있다는 것이죠.

 

예제 3: 제품 가격과 판매량의 상관관계 분석

영업팀에서 특정 제품의 가격 변동에 따른 월간 판매량 변화를 분석하여 최적의 가격 전략을 수립하고자 합니다.

데이터 (price_sales.csv):

기간,제품가격(만원),월간판매량(개)
1분기,50,200
2분기,48,220
3분기,52,190
4분기,45,250
5분기,55,180
6분기,47,230
7분기,53,185
8분기,46,240
9분기,51,195
10분기,49,210
11분기,54,182
12분기,44,260

엑셀 사용:

• A열에 '기간', B열에 '제품가격(만원)', C열에 '월간판매량(개)' 데이터를 입력합니다.
• 상관 계수를 계산할 셀에 다음 수식을 입력합니다: =PEARSON(B2:B13, C2:C13)

예제3: 엑셀 PEARSON 함수 음의 피어슨 상관관계

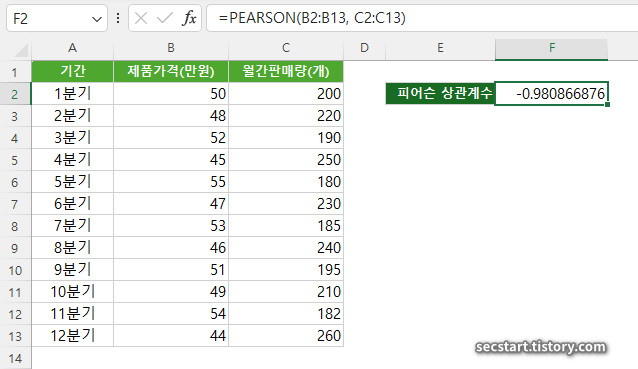
결과 해석:

만약, 결과값이 -0.92와 같이 -1에 가깝게 나왔다면, 제품 가격과 판매량 사이에 매우 강한 음의 상관관계가 있다고 해석할 수 있습니다. 즉, 가격이 올라가면 판매량은 감소하고, 가격이 내려가면 판매량은 증가하는 경향이 뚜렷하다는 의미입니다.

 

😥 PEARSON 함수 사용 시 흔한 오류들, 걱정 마세요!

PEARSON 함수를 사용하다 보면 몇 가지 오류 메시지를 만날 수 있어요. 당황하지 않고 해결할 수 있도록 주요 오류와 그 원인을 알려드릴게요.

1. #N/A 오류:
   • 원인: array1과 array2의 데이터 요소 개수가 서로 다를 때 발생합니다.
   • 해결: 두 배열에 동일한 개수의 데이터가 있는지 확인하고 범위를 다시 지정해 주세요.
2. #VALUE! 오류:
   • 원인: 배열 인수에 숫자로 변환할 수 없는 텍스트가 포함되어 있거나, 인수가 오류 값일 때 발생할 수 있습니다. (PEARSON 함수는 일반적으로 텍스트나 논리값을 무시하지만, 특정 상황이나 다른 함수와 중첩 사용 시 발생 가능성이 있습니다.)
   • 해결: 배열에 숫자 데이터만 포함되어 있는지 확인하고, 텍스트나 오류 값을 수정하거나 제거해 주세요.
3. #DIV/0! 오류:
   • 원인
     • array1 또는 array2가 비어 있을 때 발생합니다.
     • 어느 한 배열의 모든 값이 동일하여 표준 편차가 0일 때 발생합니다. (즉, 데이터에 변동이 전혀 없을 때)
   • 해결
     • 배열에 데이터가 올바르게 입력되었는지 확인하세요.
     • 데이터에 최소한 두 개 이상의 서로 다른 값이 포함되어 있는지 확인하세요. 상관관계를 계산하려면 데이터의 변동성이 필요합니다.

 

🎓 컴활 시험에도 PEARSON 함수가? (컴퓨터활용능력 연계)

네, 맞아요! PEARSON 함수는 컴퓨터활용능력 시험에서도 종종 출제되는 통계 함수 중 하나입니다. 특히 1급 실기 시험에서 데이터 분석 문제로 등장할 수 있어요.

 

컴활 시험에서는 주로 다음과 같은 형태로 PEARSON 함수 활용 능력을 평가합니다.

• 제시된 두 데이터 범위 간의 피어슨 상관 계수를 직접 계산하는 문제
• 상관 계수 결과를 해석하여 데이터 간의 관계를 설명하는 문제
• 다른 통계 함수(예: AVERAGE, STDEV 등)나 논리 함수(IF 등)와 함께 사용하여 특정 조건에 맞는 분석을 수행하는 문제

따라서 컴활 시험을 준비하시는 분들이라면 PEARSON 함수의 정확한 사용법과 의미를 숙지하고, 다양한 예제를 통해 응용력을 키우는 것이 중요합니다. 오늘 배운 내용이 시험 준비에도 큰 도움이 될 거예요! 😉

 

🎯 마무리하며: 데이터 분석, PEARSON 함수로 자신감 UP!

오늘은 엑셀의 PEARSON 함수에 대해 자세히 알아보았습니다. 어떠셨나요? 생각보다 어렵지 않죠? 😊

 

PEARSON 함수는 단순히 두 데이터 집합의 관계를 보여주는 것을 넘어, 우리가 데이터에 기반한 합리적인 의사결정을 내릴 수 있도록 도와주는 강력한 도구입니다. 마케팅 전략 수립, 생산 효율성 증대, 판매 예측 등 다양한 업무 분야에서 유용하게 활용될 수 있답니다.

 

이제 여러분도 엑셀에서 데이터를 마주했을 때, PEARSON 함수를 활용하여 숨겨진 인사이트를 발견하고 멋진 분석 결과를 만들어 보세요! 이 글이 여러분의 엑셀 활용 능력과 데이터 분석 역량을 한 단계 끌어올리는 데 도움이 되었기를 바랍니다.

 

이 글이 유용하셨다면, 주변 동료분들이나 친구들에게도 공유해 주세요! 함께 성장하는 즐거움을 나눠요! 🚀

 

 

작성자: 마늘빵