요즘 주식이나 채권 같은 금융 상품에 투자하거나, 회사에서 관련 재무 데이터를 다루시는 분들 많으시죠? 이럴 때 '듀레이션(Duration)'이라는 용어 때문에 골치 아팠던 적 없으신가요? 이게 단순히 '채권 만기'를 뜻하는 게 아니라서 처음엔 꽤 헷갈릴 수 있거든요.
오늘은 재무 관리나 투자 분석에서 정말 중요한 개념인 이 '듀레이션'을 엑셀로 아주 간단하게 계산하는 방법, 바로 엑셀 DURATION 함수에 대해 속 시원하게 알려드릴게요!
📌[핵심] 엑셀 DURATION 함수는 채권의 현금흐름이 회수되는 평균 기간(Macaulay 듀레이션)을 계산해, 이자율 변동에 따른 가격 민감도를 알려줍니다.
🧐 엑셀 DURATION 함수, 도대체 뭔가요?
엑셀 DURATION 함수는 재무 함수 중 하나로, 특정 채권에 투자했을 때 투자 원금(및 이자)이 회수되는 데 걸리는 가중 평균 기간을 연 단위로 계산해 줘요.
이걸 전문 용어로 '맥콜레이 듀레이션(Macaulay Duration)'이라고 부르는데요, 말이 좀 어렵죠? 쉽게 풀어드릴게요!
Q: DURATION이 그냥 '만기' 아닌가요? 🤔
A: 아니에요! 예를 들어 10년 만기 채권이 있다고 해볼게요. 만기는 10년이지만, 우리는 매년(혹은 6개월마다) '이자'를 받잖아요? DURATION은 이 중간에 받는 이자까지 모두 고려해서, "실제로 내 돈이 회수되는 평균적인 시간"이 얼마인지를 계산해 주는 거예요. 그래서 보통 만기보다는 짧게 나오죠. (단, 이자를 안 주는 채권은 만기와 DURATOIN이 같아요!)
Q: 그래서 DURATION을 아는 게 왜 중요한데요? 💰
A: 이게 바로 핵심인데요! DURATION은 '이자율 변동에 대한 채권 가격의 민감도'를 나타내는 지표이기 때문이에요.
- DURATION 수치가 높다 = 시장 이자율이 1% 변할 때 채권 가격이 더 많이, 더 민감하게 움직인다! (즉, 리스크가 더 크다!)
- DURATION 수치가 낮다 = 시장 이자율이 변해도 채권 가격이 비교적 둔감하게 움직인다! (리스크가 더 작다!)
따라서 DURATION 함수는 투자 포트폴리오의 리스크를 관리하는 데 아주 유용하게 사용된답니다.
✍️ DURATION 함수 기본 구문 파헤치기
DURATION 함수의 기본 생김새(구문)는 이렇습니다. 총 5개의 필수 인수와 1개의 선택 인수로 구성되어 있어요.
DURATION(settlement, maturity, coupon, yld, frequency, [basis])
이전 게시물에서 자주 보이던 인수들이지요. 각 인수가 뭘 의미하는지 하나씩 살펴볼까요?
- settlement (결제일) : [필수] 채권을 매입한 날짜예요. (예: 2025-01-15)
- maturity (만기일) : [필수] 채권이 만기되어 원금을 돌려받는 날짜예요. (예: 2030-01-15)
- coupon (표면 이자율) : [필수] 채권 증서에 적힌 연간 이자율이에요. (예: 5%라면 0.05 또는 5%로 입력)
- yld (수익률) : [필수] 채권의 연간 만기 수익률(시장 이자율)을 의미해요. (예: 6%라면 0.06 또는 6%로 입력)
- frequency (이자 지급 빈도) : [필수] 1년에 이자를 몇 번 주는지 숫자로 입력해요.
1 : 연 1회 지급
2 : 연 2회 지급 (반기)
4 : 연 4회 지급 (분기)
- [basis] (날짜 계산 기준) : [선택] 날짜 계산 방식을 정해요. 보통 생략하거나 0 (미국식 30/360 기준)을 가장 많이 사용합니다.
| Basis | Day count |
|---|---|
| 0 or 생략 (기본값) | 미국 (NASD) 30/360 |
| 1 | 실제/실제 |
| 2 | 실제/360 |
| 3 | 실제/365 |
| 4 | 유럽 30/360 |
[노트 💡] 정말 중요한 점!
settlement (결제일)와 maturity (만기일) 인수는 반드시 엑셀이 인식하는 날짜 형식 (예: 2025-01-15)이거나 DATE(2025, 1, 15)와 같은 함수 형식이어야 해요. 만약 "2025년 1월 15일" 같은 텍스트로 입력하면 #VALUE! 오류가 발생하니 꼭 주의하세요!
💻 엑셀 DURATION 함수 실전 예제 (feat. CSV 데이터)
자, 이제 실제 데이터를 가지고 DURATION 함수를 사용해 볼게요. 아래 데이터를 복사해서 엑셀 시트 A1 셀에 붙여넣기 해보세요!
채권명,결제일,만기일,표면이자율,시장수익률,이자지급,지급횟수(frequency)
A-1채권,2025-01-15,2030-01-15,5.0%,6.0%,연1회,1
B-2채권,2025-01-15,2030-01-15,5.0%,6.0%,연2회,2
C-3채권,2025-01-15,2035-01-15,5.0%,6.0%,연2회,2
D-4채권,2025-01-15,2030-01-15,8.0%,6.0%,연2회,2
E-5채권,2025-03-01,2028-03-01,4.0%,4.5%,연4회,4
F-6채권,2025-06-01,2032-06-01,7.0%,6.5%,연1회,1
G-7채권(제로쿠폰),2025-01-01,2030-01-01,0.0%,5.0%,연1회,1(데이터가 잘 복사되도록 지급횟수(frequency) 열(G열)을 추가했어요!)
예제 1: 기본 사용법 (연 1회 이자 지급)
시나리오: A-1 채권 (만기 5년, 표면이자율 5%, 시장수익률 6%, 연 1회 이자 지급)의 DURATION을 계산해봅니다.
수식: I2 셀에 아래와 같이 입력하세요.
=DURATION(B2, C2, D2, E2, G2)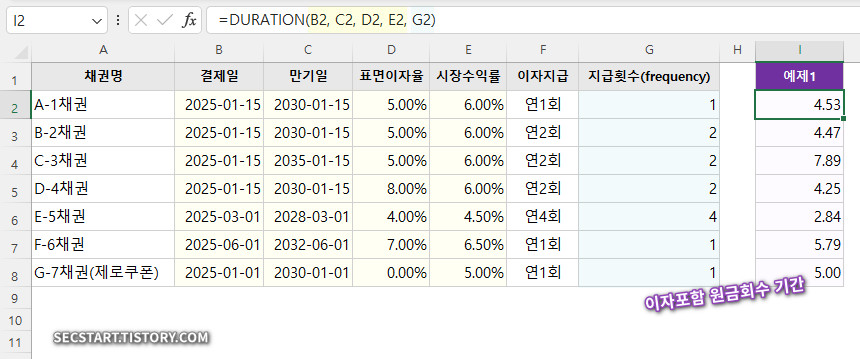
결과: 약 4.53년
해석: 이 채권의 만기는 5년이지만, 매년 받는 이자를 고려한 실제 자금 회수 기간(DURATION)은 약 4.53년이라는 의미입니다.
예제 2: 중급 활용 (연 2회 이자 지급 - 가장 일반적!)
시나리오: B-2 채권. 모든 조건은 A-1 채권과 같지만, 이자 지급만 연 2회(반기)로 다릅니다.
수식: I3 셀에 아래와 같이 입력하세요.
=DURATION(B3, C3, D3, E3, G3)
결과: 약 4.47년
해석: 어? 결과가 줄었죠? 이자를 1년에 2번, 즉 더 자주 받으니까 돈이 더 빨리 회수되는 셈이에요. 그래서 DURATION(자금회수기간)이 4.47년으로 A-1 채권보다 약간 짧아졌어요.
예제 3: 실무 활용 (채권 리스크 비교 분석)
시나리오: B-2 채권(만기 5년)과 C-3 채권(만기 10년) 중 어떤 채권이 이자율 변동에 더 민감할까요? (두 채권 모두 이자 지급 횟수는 연 2회)
수식 1 (B-2): I3 셀 (결과: 4.47년)
=DURATION(B3, C3, D3, E3, G3)
수식 2 (C-3): I4 셀에 입력
=DURATION(B4, C4, D4, E4, G4)결과 (C-3): 약 7.89년
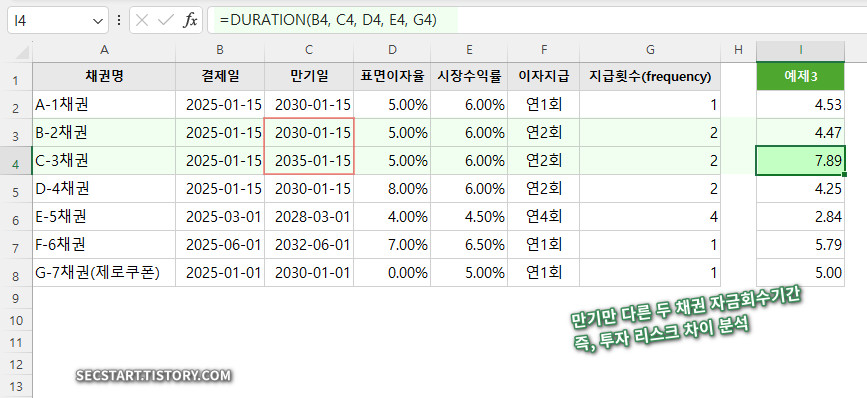
실무 분석:
-B-2 채권 DURATION: 4.50년
-C-3 채권 DURATION: 7.80년
-C-3 채권의 DURATION이 B-2 채권보다 훨씬 길죠?
결론: 만약 앞으로 시장이자율이 상승할 것 같다 (수익률 'yld'가 올라간다)면, DURATION이 더 긴 C-3 채권의 가격이 B-2 채권보다 더 많이 하락할 위험이 큽니다.
이게 바로 실무에서 DURATION을 계산하고 비교하는 핵심 이유랍니다!
🚨 DURATION 함수, 이럴 때 오류 나요! (오류 해결)
함수를 쓰다 보면 오류가 날 때도 있죠? DURATION 함수는 이럴 때 오류가 나요!
- #VALUE! 오류
- 가장 흔한 오류예요!
- 원인: settlement (결제일) 또는 maturity (만기일) 인수에 날짜 형식이 아닌 텍스트 값이 입력되었을 때 발생합니다.
- 해결: DATE 함수를 쓰거나, 2025-10-23과 같이 엑셀이 인식하는 날짜 형식으로 고쳐주세요.
- #NUM! 오류
- 숫자 관련 오류라는 뜻이죠.
- 원인 1: coupon (이자율)이나 yld (수익률)이 0보다 작을 때 (음수일 때)
- 원인 2: frequency (이자 지급 빈도)가 1, 2, 4 이외의 숫자가 입력되었을 때
- 원인 3: settlement (결제일)이 maturity (만기일)보다 크거나 같을 때 (즉, 결제일이 만기일보다 늦을 때)
- 해결: 각 인수에 올바른 숫자와 날짜 순서를 입력했는지 다시 한번 꼼꼼히 확인해 보세요!
📚 함께 알면 좋은 관련 함수들
DURATION 함수를 배웠다면, 이 함수들과도 금방 친해질 수 있어요!
- MDURATION 함수: '수정 듀레이션(Modified Duration)'을 계산해 줘요. DURATION이 '기간'에 초점을 맞췄다면, MDURATION은 '이자율 1% 변동 시 채권 가격이 몇 % 변하는지'를 더 직접적으로 보여주는 지표라서 실무에서 훨씬 더 많이 쓰일 수도 있어요!
- PRICE 함수: 채권의 현재 가격(100원당)을 계산할 때 사용해요.
- YIELD 함수: 반대로 채권 가격을 알 때, 만기 수익률(yld)을 역으로 계산할 때 사용합니다.
✔ 마무리하며
오늘은 엑셀 재무 함수 중에서도 조금 전문적이지만 아주 중요한! DURATION 함수에 대해 알아봤어요. 📈
단순히 '기간'을 계산하는 함수가 아니라, 채권 투자의 핵심 리스크 지표인 '이자율 민감도'를 파악하는 열쇠라는 점! 이제 확실히 이해되셨죠?
처음엔 용어들이 조금 생소하고 어렵게 느껴질 수 있어요. 하지만 오늘 배운 대로 함수 구문과 예제를 몇 번만 직접 따라 입력해 보시면, "아! 이게 이 뜻이었구나!" 하고 금방 익숙해지실 거예요.
오늘 내용이 여러분의 재무 지식과 엑셀 실력 향상에 조금이나마 도움이 되었기를 바랍니다!
내용이 유익하셨다면 공감(❤️)과 댓글 꼭 부탁드리고요, 재무팀 동료나 투자 스터디 친구들에게 공유해주시는 것도 저에게 큰 힘이 됩니다! 😉
그럼 저는 다음에 더 유용한 게시물로 돌아올게요! 감사합니다.
📱 모바일에서 빠르게 보는 DURATION 함수 핵심 요약
- 용도: 채권의 평균 자금 회수 기간 (Macaulay 듀레이션) 계산
- 핵심: 이자율 변동에 대한 가격 민감도 (리스크) 측정 (결과 숫자가 클수록 리스크 UP!)
- 구문: =DURATION(결제일, 만기일, 표면이자율, 시장수익률, 연간이자지급횟수, [기준])
- 필수 인수:
- 결제일, 만기일: 날짜 형식 (예: 2025-01-15)
- 이자율(coupon), 수익률(yld): 소수점 혹은 %단위 (예: 5%, 0.05)
- 이자지급횟수(frequency): 1(연1회), 2(연2회), 4(연4회)
- 주의!