안녕하세요! 😊
엑셀로 재무 관리나 투자 분석을 하시다 보면, 특히 '채권'을 다룰 때가 있는데요. 채권 투자의 가장 큰 적! 바로 '이자율(금리) 변동'이죠. 😱 금리가 1% 오르면 내가 가진 채권 가격은 얼마나 떨어질까? 이 위험을 정확히 숫자로 알고 싶을 때가 많으셨을 거예요.
오늘은 바로 이 '이자율 변동에 대한 채권 가격의 민감도'를 측정하는 아주 중요한 재무 함수, 엑셀 MDURATION 함수에 대해 쉽고 자세하게 알려드릴게요!
📌 [핵심] MDURATION 함수는 이자율(수익률)이 1% 변할 때 채권 가격이 약 몇 % 변하는지(수정 듀레이션)를 계산해주는 재무 함수예요.
📈 엑셀 MDURATION 함수, 대체 뭔가요?
MDURATION 은 'Modified Duration'의 약자, 우리말로는 '수정 듀레이션'이라고 불러요.
🤔 듀레이션(Duration)? 그게 뭔데요?
쉽게 말해 채권 투자 원금을 회수하는 데 걸리는 평균 시간(가중평균만기)을 의미하는데요, 이 듀레이션은 이자율 변화에 채권 가격이 얼마나 민감하게 반응하는지 보여주는 척도로도 사용돼요.
여기서 MDURATION (수정 듀레이션)은 한발 더 나아가, "만기 수익률(YTM)이 1% (또는 100bp) 변동할 때 채권 가격이 몇 퍼센트(%) 변동하는지"를 직접적으로 보여주는 값입니다.
예를 들어, 어떤 채권의 MDURATION 값이 '5'가 나왔다면?
- 이자율(수익률)이 1% 상승하면 ➡️ 채권 가격은 약 5% 하락 📉
- 이자율(수익률)이 1% 하락하면 ➡️ 채권 가격은 약 5% 상승 📈
한다는 의미죠. 투자 위험 관리에 정말 필수적인 지표랍니다!
📝 [참고]
위에서 bp는 'Basis Point(베이시스 포인트)'의 약자입니다.
금융 분야, 특히 금리(이자율)나 채권 수익률처럼 아주 미세한 변화를 다룰 때 사용하는 '최소 단위'라고 생각하시면 쉬워요.
- 1 bp = 0.01% (즉, 1%의 100분의 1)
- 100 bp = 1%
왜 % 대신 bp를 쓸까요?
금융 시장에서는 0.25%, 0.5%처럼 소수점 단위로 금리가 변동하는 경우가 아주 흔한데요,
- "금리가 0.25%포인트 올랐습니다."
- "금리가 25bp 올랐습니다."
이렇게 말할 때, 'bp' 단위를 쓰면 소수점 없이 정수로 깔끔하게 표현할 수 있고, "0.25%가 올랐다"와 "25%가 올랐다"처럼 헷갈릴 수 있는 실수를 줄여주기 때문에 현업에서 아주 즐겨 사용한다고 해요!
🔍 MDURATION 함수 구문과 인수 살펴보기
엑셀 MDURATION 함수의 기본 생김새(구문)는 이렇습니다.
=MDURATION(settlement, maturity, coupon, yld, frequency, [basis])인수가 좀 많아 보이지만, 재무 함수는 인수가 대부분 비슷해요. 하나씩 살펴볼게요!
| 인수 | 설명 | 필수/선택 |
|---|---|---|
| settlement | 결제일 (매입일): 채권을 실제로 구매한 날짜예요. (유통일) | 필수 |
| maturity | 만기일: 채권의 원금과 마지막 이자를 받는 날짜죠. | 필수 |
| coupon | 표면 이자율: 채권에 적혀있는 연간 이자율이에요. (예: 5% -> 0.05) | 필수 |
| yld | 수익률 (YTM): 해당 채권의 만기 수익률(Yield To Maturity)입니다. (예: 4.5% -> 0.045) | 필수 |
| frequency | 연간 이자 지급 횟수: 1 (연 1회), 2 (반기, 연 2회), 4 (분기, 연 4회) 중 하나를 숫자로 입력해요. | 필수 |
| [basis] | 날짜 계산 기준 (선택): 날짜 계산 방식을 정해요. 생략하거나 0을 쓰면 미국식(30/360) 기준입니다. (1: 실제/실제, 2: 실제/360, 3: 실제/365, 4: 유럽식 30/360) | 선택 |
📝 중요 노트!
- settlement (결제일) 와 maturity (만기일) 은 반드시 엑셀이 인식하는 날짜 형식이어야 해요. (예: "2024-10-25" 또는 DATE(2024, 10, 25) 함수 사용)- coupon 과 yld 는 퍼센트(%)가 아닌 소수점 형태 (예: 3.5% ➡️ 0.035)로 입력해야 정확해요.
- frequency 는 반드시 1, 2, 4 중 하나의 정수여야 합니다!
📊 MDURATION 함수 실전 예제 (데이터 포함)
자, 이제 실제 업무에서 사용할 법한 데이터로 MDURATION 함수를 연습해 볼게요.
아래는 가상의 채권 포트폴리오 데이터입니다.
채권명,결제일,만기일,표면이율,수익률,이자지급(회),날짜기준
국고채 A,2024-01-15,2029-01-15,0.035,0.040,2,1
회사채 B,2023-05-10,2028-05-10,0.050,0.045,2,0
국고채 C,2024-03-01,2034-03-01,0.030,0.038,1,1
회사채 D,2023-11-20,2026-11-20,0.042,0.040,2,0
특수채 E,2024-06-01,2027-06-01,0.038,0.039,4,1
회사채 F,2023-09-01,2030-09-01,0.045,0.048,2,0
국고채 G,2024-02-15,2027-02-15,0.028,0.035,1,1
회사채 H,2023-12-30,2025-12-30,0.055,0.050,4,0(위 데이터를 엑셀 시트 A1:G9 범위에 복사해서 붙여넣고 [데이터] - [텍스트 나누기] - [쉼표(,)로 구분]을 실행하면 표로 만들어져요!)
예제 1: 기본 사용법 (국고채 A)
A2:G2 범위의 '국고채 A' 데이터를 이용해 MDURATION을 계산해봅니다.
- 결제일(B2): 2024-01-15
- 만기일(C2): 2029-01-15
- 표면이율(D2): 0.035 (3.5%)
- 수익률(E2): 0.040 (4.0%)
- 이자지급(F2): 2 (반기)
- 날짜기준(G2): 1 (실제/실제)
[I2 셀에 입력할 수식]
=MDURATION(B2, C2, D2, E2, F2, G2)

[결과]
약 4.534 가 나옵니다. (소수점 자릿수에 따라 다를 수 있어요)
예제 2: 날짜를 DATE 함수로 직접 입력 / 회사채 B
만약 데이터가 셀에 없고, 날짜를 직접 입력해야 한다면 DATE 함수를 쓰는 것이 가장 안전해요. '회사채 B' 의 정보를 이용해볼게요.
- 결제일: 2023-05-10 ➡️ DATE(2023, 5, 10)
- 만기일: 2028-05-10 ➡️ DATE(2028, 5, 10)
- 표면이율: 0.05
- 수익률: 0.045
- 이자지급: 2
- 날짜기준: 0
[임의의 셀에 입력할 수식]
=MDURATION(DATE(2023, 5, 10), DATE(2028, 5, 10), 0.05, 0.045, 2, 0)
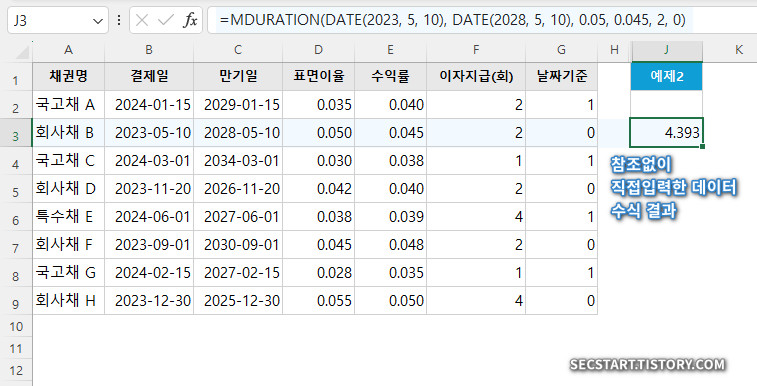
[결과]
약 4.393 이 계산됩니다.
예제 3: 이자 지급 횟수 비교 / 국고채 C vs 특수채 E
이자 지급 횟수(frequency)가 듀레이션(투자금 회수기간)에 어떤 영향을 미치는지 비교해볼까요?
ㄱ. 국고채 C (연 1회 지급)
=MDURATION(B4, C4, D4, E4, F4, G4)[결과] 약 8.416
ㄴ. 특수채 E (분기 4회 지급)
=MDURATION(B6, C6, D6, E6, F6, G6)[결과] 약 2.822

(만기나 수익률이 다르긴 하지만) 일반적으로 다른 조건이 동일하다면, 이자를 자주 지급할수록(frequency 숫자가 클수록) 원금 회수가 빨라지므로 듀레이션(MDURATION) 값은 짧아지는(작아지는) 경향이 있어요.
예제 4: 실무 활용 (결과 해석하기!) ⭐️
이게 제일 중요하죠! "그래서 이 숫자가 무슨 뜻인데?"

예제1 에서 계산한 '국고채 A'의 MDURATION 값 4.534 를 해석해 봅시다.
- 해석: 이 채권(국고채 A)은 현재 시장 금리(수익률)가 1% (100bp) 상승할 경우, 채권 가격이 약 4.534% 하락할 것으로 예상됩니다.
- 반대로: 시장 금리가 1% 하락하면, 채권 가격은 약 4.352% 상승할 것으로 예상됩니다.
MDURATION 값이 클수록 이자율 변동에 가격이 더 민감하게 반응(위험이 크다)하고, 값이 작을수록 덜 민감하게 반응(위험이 작다)한다는 뜻이에요.
📝 [노트]
엑셀의 MDURATION 함수가 반환하는 값은 '회수 기간(시간)'이 아니라, '가격 민감도(%)'를 의미합니다.
- MDURATION (수정 듀레이션): 이자율 1% 변동 시 가격이 몇 % 변하는지 (가격 민감도 '%' 📉📈)
- DURATION (매콜레이 듀레이션): 투자 원금을 회수하는 데 걸리는 평균 시간 (회수 기간 '년(Year)' 🗓️)
그래서 MDURATION 결과값이 '5' 가 나왔다면, "5년 걸린다" 가 아니라 "이자율 1% 변할 때 가격이 5% 움직인다" 라고 해석하는 것이 맞습니다!
🚨 MDURATION 함수, 이럴 때 오류 나요! (오류 해결)
함수를 쓰다 보면 오류가 발생할 수 있죠. 당황하지 마세요!
- #NUM! 오류:
- settlement (결제일)이 maturity (만기일)보다 나중 날짜일 때.
- coupon (표면이율)이나 yld (수익률)가 0보다 작을 때 (음수일 때).
- frequency (이자 지급 횟수)가 1, 2, 4가 아닌 다른 숫자일 때 (예: 3).
- basis (날짜 기준)가 0, 1, 2, 3, 4 이외의 숫자일 때.
- #VALUE! 오류:
- settlement 또는 maturity가 유효한 날짜 형식이 아닐 때 (예: 텍스트로 "2024년 1월 15일"이라고 입력).
- 다른 인수들(coupon, yld, frequency, basis)이 숫자가 아닌 텍스트일 때.
🔗 함께 알면 좋은 재무 함수들
MDURATION을 사용하신다면 아래 함수들도 분명 필요하실 거예요!
- DURATION: 수정 듀레이션(MDURATION)의 기반이 되는 '매콜레이 듀레이션(Macaulay Duration)'을 계산합니다. (원금 회수 기간)
- PRICE: 수익률(YTM)을 알 때 채권의 현재 가격을 계산합니다.
- YIELD: 채권의 현재 가격을 알 때 만기 수익률(YTM)을 계산합니다. (PRICE와 반대)
- ACCRINT: 결제일(매입일)까지 발생한 경과 이자를 계산합니다.
🙋♀️ 마무리하며
어떠셨나요? 엑셀 MDURATION 함수, 이름은 조금 어려웠지만 알고 보니 채권 투자의 위험을 관리하는 데 정말 강력하고 유용한 도구죠? 🤓
특히 포트폴리오에 채권을 담고 계시거나, 재무/회계 관련 업무를 하신다면 이자율 변동에 따른 자산 가치 변화를 예측하기 위해 MDURATION(수정 듀레이션) 개념은 꼭 알아두셔야 해요. 오늘 배운 예제 데이터를 활용해서 직접 엑셀에 입력해보고, 숫자도 바꿔보면서 꼭 손에 익혀보시길 바라요!
오늘 내용이 여러분의 엑셀 실무 능력 향상에 도움이 되었다면 공감(❤️)과 댓글 잊지 마시고요! 궁금한 점이나 다음에 다뤄줬으면 하는 엑셀 함수가 있다면 언제든 편하게 남겨주세요.
그럼 우린 다음 엑셀 게시물로 또 만나요! 👋
📱 바쁘신 분들을 위한 [MDURATION 함수] 모바일 요약
1. MDURATION 함수란?
'수정 듀레이션' (Modified Duration) 계산.
핵심: 이자율(수익률) 1% 변동 시 채권 가격이 몇 % 변하는지 알려줌.
(예) MDURATION = 3 이면 ➡️ 금리 1% 오르면 가격 3% 하락.
2. 함수 구문
=MDURATION(결제일, 만기일, 표면이율, 수익률, 이자지급횟수, [날짜기준])
3. 필수 인수
settlement : 결제일, 채권 산 날 (날짜 형식!)
maturity : 만기일, 채권 끝나는 날 (날짜 형식!)
coupon : 표면 이율 (예: 5% -> 0.05)
yld : 만기 수익률 (예: 4.5% -> 0.045)
frequency : 연 이자 지급 횟수 (숫자 1, 2, 또는 4)
4. 자주 나는 오류
#NUM! : 결제일 > 만기일 경우, 이율/수익률 < 0 경우, frequency가 1/2/4가 아닌 경우.
#VALUE! : 날짜가 텍스트임, 숫자가 텍스트임.
5. 실무 활용 팁
- MDURATION 값이 클수록 금리 변동에 민감 (위험 큼).
- MDURATION 값이 작을수록 금리 변동에 둔감 (위험 작음).
채권 포트폴리오의 위험 관리에 필수!